1) 固有振動数と固有周期
地震,風,車両などで橋梁などの構造物が揺れる場合
構造物は特定の振動数に対してのみ激しく揺れる性質があります。
この振動数は構造物によって異なりますので,構造物の固有振動数と言います。
固有振動数の逆数を構造物の固有周期と言います。
一般に固有振動数(固有周期)は複数あります。
固有振動数(固有周期)は固有値解析と言う数学的な手法で求めることができます。
橋梁のような大規模構造物では固有振動数(固有周期)はたくさんあり、
小さいものから第1次固有振動数、第2次固有振動数、・・・、
大きいものから第1次固有周期、第2次固有周期、・・・
と名付けます。
2)刺激係数
構造物は複数あるすべての固有振動数(固有周期)で激しく揺れるわけではありません。
どの固有周期(固有振動数)で激しく揺れるかを見極めるためには刺激係数に着目します。
刺激係数は地震動に対する揺れの感度とでも言うべきもので固有値解析で求めることができます。
刺激係数(一般的には正,負の値となります。)の絶対値が大きいほど激しく揺れます。
刺激係数の数学的な説明は以下のリンクにあります。
⑤レイリー減衰
3)卓越固有振動数,卓越固有周期
刺激係数の絶対値の大きい固有振動数(固有周期)を卓越固有振動数(卓越固有周期)と言います。
4)地震動の卓越振動数(卓越周期)

もちろん地震動の卓越振動数(卓越周期)は地震動により異なります。
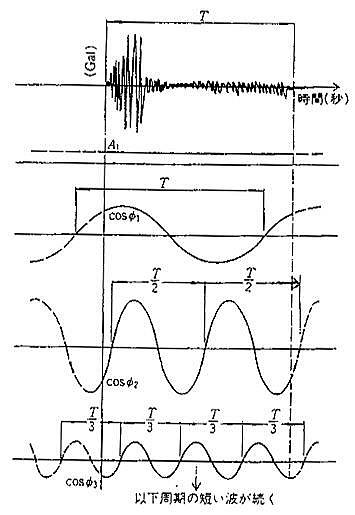
図-1 地震動の振動数成分
5) 共振


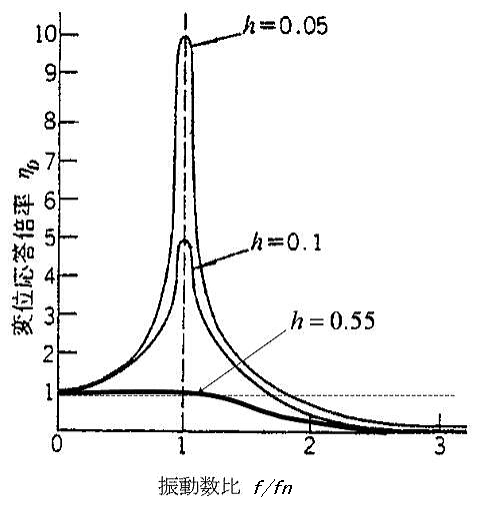
図-2 振動数比-変位応答倍率曲線(共振曲線)
共振時の振動形状を卓越モードと言います。
斜張橋、つり橋や高橋脚ラーメン橋などの複雑な構造物では卓越振動数は1つではなく複数あります。
つまりこのような橋は長周期の地震動で共振するばかりでなく、それより短い周期の地震動でも共振する
場合があるのです。
6)平成28年熊本地震
平成28年熊本地震では地震動の卓越振動数と民家の固有振動数が
近接していたので、共振現象により甚大な被害が民家に発生したと考えられます。
7)座屈拘束低降伏点鋼が大きな制振効果を有する理由
座屈拘束低降伏点鋼のエネルギー吸収度合を滅衰定数で表したものを等価減衰定数
(リンク参照)と言います。
座屈拘束低降伏点鋼の等価減衰定数は55%程度です。
橋の滅衰定数をh=0.05 としますと、座屈拘束低降伏点鋼を取り付けた場合、
地震時の応答は反比例しますから、応答は1/10程度になります。(図-2参照)
これを静力学で考えると、作用する地震力は1/10になるということです。
座屈拘束低降伏点鋼が大きな制振効果を有することがわかります。